图的基本知识

Posted on | In | 本文总阅读量 次

图的基本知识

稀疏矩阵的存储方式

Coordinate（COO）

​ 这是最简单的一种存储格式，每一个元素需要使用一个三元组来表示，分别是（行号，列号，数值），一个例子，如下：

1
2
3
4
5
6
7
8
9
10
11
12
6, 0, 8, 0
0, 7, 0, 0
0, 0, 0, 0
0, 0, 0, 5
对应的存储矩阵如下
0, 0, 6
3, 3, 5
1, 1, 7
0, 2, 8
即row = [0, 3, 1, 0]
  col = [0, 3, 1, 2]
  data = [6, 5, 7, 8]

Compressed Sparse Column（CSC）

​ CSC是按列进行存储的，其中indptr中的数据代表矩阵中每一列所存的数据在data中的开始和结束的索引，例如下面的indptr为[0, 2, 3, 6]，即表示在data中，索引[0, 2)为第一列的数据，索引[2, 3)为第二列的数据，索引[3, 6)为第三列的数据。而indices中的数据代表data数据对应的行（len(data) = len(indices)）。例如，这里的indices为[0, 2, 2, 0, 1, 2]，代表data中数据1在第0行，数据2在第2行，数据3在第2行，数据4在第0行，数据5在第一行，数据6在第2行。从而建立起一个稀疏矩阵。

1
2
3
4
5
6
7
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csc_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 4],
       [0, 0, 5],
       [2, 3, 6]])

Compressed Sparse Row（CSR）

​ CSR是按行来进行存储稀疏矩阵的，其原理和CSC类似。indptr中的数据表示矩阵中的每一行在data中的开始和结束索引，而indices表示data数据所在的列数。一个例子如下：

1
2
3
4
5
6
7
>>> indptr = np.array([0, 2, 3, 6])
>>> indices = np.array([0, 2, 2, 0, 1, 2])
>>> data = np.array([1, 2, 3, 4, 5, 6])
>>> sparse.csr_matrix((data, indices, indptr), shape=(3, 3)).toarray()
array([[1, 0, 2],
       [0, 0, 3],
       [4, 5, 6]])

同构图和异构图

​ 在同构图中，所有节点表示同一类型的实体，所有边表示同一类型的关系。例如，社交网络的图由表示同一实体类型的人及其相互之间的社交关系组成。在异构图中，节点和边的类型可以不同。例如，市场的图可以有表示“顾客”、“商家”和“商品”的节点，它们通过“想购买”、“已经购买”、“是顾客”和“正在销售”的边进行相互连接。二分图是一种特殊的、常用的异构图，其中的边连接两类不同类型的节点。例如，在推荐系统中，可以使用二分图表示“用户”和“物品”之间的关系。

图的一些属性

特征向量中心性

考虑了自己的度以及它连接节点的度：$A*x = \lambda *x$ 。

中介中心性

$$
Betweenness = \frac{经过该节点的最短路径}{其余两两节点的最短路径}
$$

中介中心性和介数类似，只不过上下都是总数

连接中心性

$$
Closeness = \frac{n-1}{节点到其他节点最短路径之和}
$$

图的一些算法

PageRank

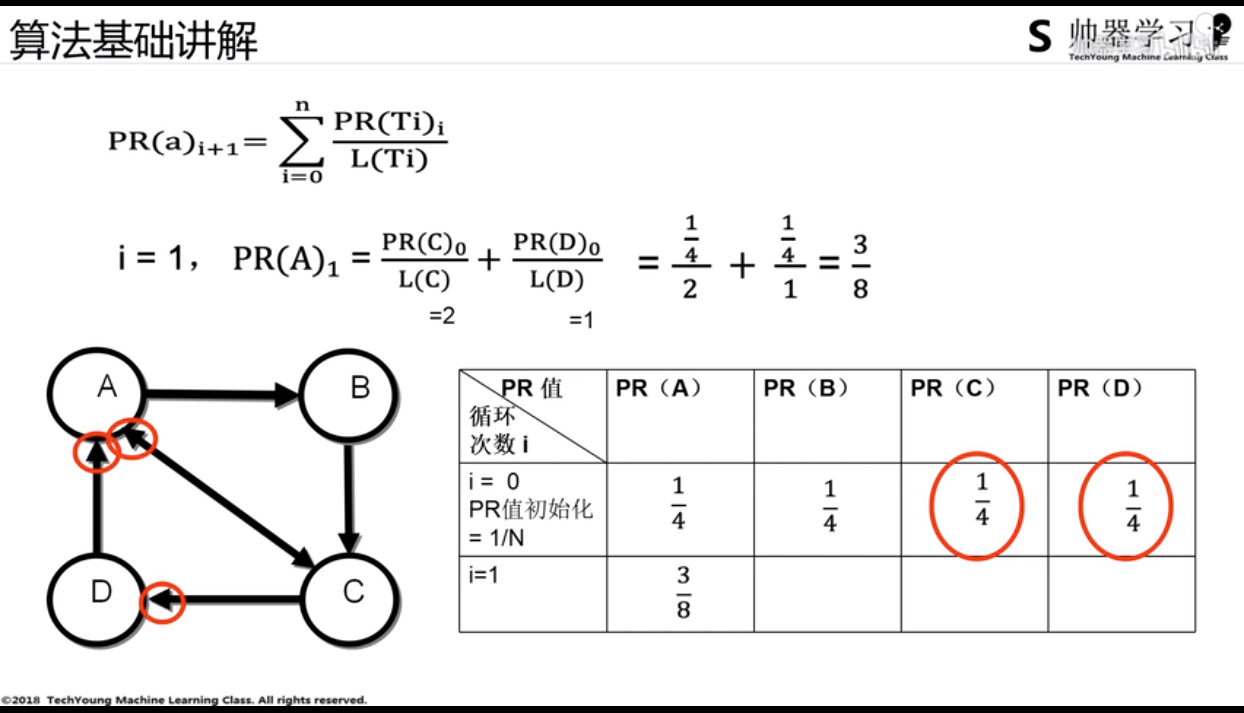
节点a的PageRank值计算如下：
$$
PR(a){i+1}=\sum{i=0}^n\frac{PR(Ti)_i}{L(Ti)}
$$

  • $PR(Ti)$代表的是其他节点（指向a节点的节点）的PR值
  • $L(Ti)$代表的是其他节点（指向a节点的节点）的出度数
  • $i$代表的是循环次数

下面是PageRank的一个实例，PageRank在多次迭代之后会逐渐收敛。

PageRank实例